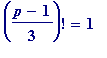Abstract

"A theorem is never arrived at in the way that logical
thought would lead you to believe or that posterity thinks.
It is usually much more accidental, some chance discovery
in answer to some kind of question. Eventually you can
rationalise and say that this is how it fits.

Discoveries never happen as neatly as that.

You can rewrite history and make it look more

logical, but actually it happens quite differently."

Michael Atiyah (from M. Raussen and C. Skau, Interview with

Michael Atiyah and Isadore Singer, Notices of the American

Mathematical Society, Feb 2005, Vol. 52, Number 2, 225-233)

In this talk I will sketch some of the questions and chance discoveries that led me to discovering the theorems below (over a period of days, between Tues 23rd Nov and Wed 15th Dec 2004)

The renowned number theorist Andrew Granville provided some proofs based on classical work of Gauss and Jacobi, beautifully detailed in: B. C. Berndt, R. J. Evans, and K. S. Williams, Gauss and Jacobi Sums , Canadian Mathematical Society Series of Monographs and Advanced Texts, Volume 21, Wiley-Interscience (1998)

There are infinitely many primes p = 1 (mod 3):

7, 13, 19, 31, 37, 43, 61, 67, 73, 79, 97, 103, 109, 127, � (1)

Of those, every one of the following

3571, 4219, 13669, 25117, 55897, 89269, 102121, 170647, � (2)

satisfies the congruence

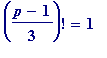(mod p ) (3)

and every one of these

7, 61, 331, 547, 1951, 2437, 7351, 8269, 9241, 10267, 23497, � (4)

satisfies

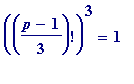(mod p ) (5)

but not (3).

Finally, every one of

19, 37, 127, 271, 397, 631, 919, 1657, 1801, 2269, 2791, � (6)

satisfies

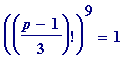(mod p ) (7)

but neither of the congruences (3) nor (5).

In short, primes in the sequences (2), (4) and (6) satisfy respectively (where is the number theoretic function the order of a modulo n , the smallest positive integral power of a that is congruent to 1 mod n ).

None of the sequences (2), (4) or (6) have - so far as I know - been previously identified; certainly none are listed at N. J. A. Sloane's well-known On-Line Encyclopaedia of Integer Sequences

http://www.research.att.com/~njas/sequences/

(See, too, Sloane's wonderful article: The On-Line Encyclopaedia of Integer Sequences, Notices of the American Mathematical Society , Sept 2003, Vol. 50, Number 8, 912-915)

Holding the view that all primes having significant properties should be named, I would like to name the primes in (2), (4) and (6) as being Jacobi primes of order 1, 3 and 9 respectively (the reason for that should be clear later...). It was those of order 1 and 3 that I originally sought; those of order 9 emerged as a bonus.

I hope the following will come as a surprise:

Theorem 1 . A prime p = 1 (mod 3) is a Jacobi prime of order 1 or 3 if and only if

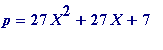
for some integer X , while p is a Jacobi prime of order 9 if and only if

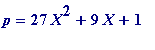or

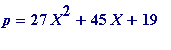
for some integer X. ( Two sequences produced by one polynomial; one sequence produced by two !)

Furthermore, letting be the least absolute residue of 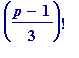mod p , then, whenever , one has

Theorem 2 . There are no primes p = 1 (mod 3) satisfying

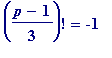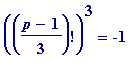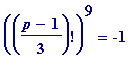(mod p ), (mod p ) or (mod p )